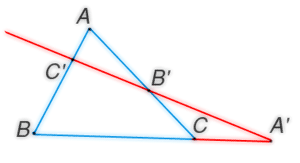
Теорема Менелая
Рисунки и закономерности
Теорема Менелая. Доказательства
Решение задач с помощью теоремы Менелая
Решите самостоятельно
В курсе геометрии есть теоремы, которые изучаются в школе недостаточно подробно, но которые
могут быть полезны для решения наиболее сложных задач ОГЭ и ЕГЭ. К ним относится, например, теорема Менелая. Традиционно она изучается в классах с углублённым изучением
математики в 8-м классе, а в обычной программе (по учебнику Атанасяна) теорема Менелая включена в учебник 10-11 классов.
Между тем результат штудирования Интернет-ресурсов, упоминающих теорему Менелая, показывает, что обычно она
формулируется неполно и потому неточно, а все случаи её использования, равно как и доказательство обратной теоремы не приводятся. Цель настоящей статьи — разобраться, что
такое теорема Менелая, как и для чего она используется, а также поделиться методикой преподавания этой теоремы на индивидуальных занятиях репетитора с учениками.
Рассмотрим типовую задачу (Задание № 26, ОГЭ), встречающуюся на экзаменах во множестве вариантов, отличающихся только числами в условии.
|
Задача 1. Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 17. Найдите основания трапеции. |
|---|
Решение самой задачи несложное – ознакомиться с ним можно ниже. В настоящей же статье нас интересует главным образом немножко другой
момент, который зачастую опускается, понимается, как сам собой разумеющийся, как очевидный. Но очевидное — это то, что можно доказать. А доказать это можно различными способами,
— обычно доказывают исключительно с помощью подобия, — но можно и с помощью теоремы Менелая.
Из условия следует, что, так как углы при нижнем основании трапеции в сумме составляют 90°, то если продлить боковые
стороны, получится прямоугольный треугольник. Далее из получившейся точки пересечения продолжений боковых сторон проводят отрезок, который проходит через середины оснований.
А почему этот отрезок проходит через все эти три точки? Обычно об этом в решениях задачи, встречающихся в Интернете, не говорится ни слова. Отсутствует даже отсылка к теореме
о четырёх точках трапеции, не говоря уже о доказательстве этого утверждения. А между тем, оно может быть доказано с помощью теоремы Менелая, которая представляет собой условие
принадлежности трёх точек к одной прямой. Продолжение решения задачи…
Настало время сформулировать теорему. Надо отметить, что в различных учебниках
и пособиях встречаются довольно-таки разные её формулировки, хотя суть остаётся неизменной.
В учебнике Атанасяна и др. за 10-11 классы приводится такая формулировка теоремы Менелая, назовём её «векторной»:
|
|
|---|
а в учебнике тех же авторов «Геометрия. 8 класс. Дополнительные главы к учебнику» — наряду с этой же «векторной» формулировкой (на с. 190), в качестве теоремы Мепнелая даётся следствие из неё
для отрезков (на с. 92):
|
Если на сторонах AB и BC и продолжении стороны AC (либо на продолжениях сторон AB, BC и AC) взяты соответственно точки C1, A1 и B1, то эти точки лежат на одной прямой тогда и только тогда, когда |
|---|
В учебнике «Геометрия 10-11 класс» Александрова и др., а также в учебном пособии этих же авторов
«Геометрия. 8 класс» приводится несколько иная формулировка теоремы Менелая, причём и для 10-11 классов и для 8 класса она одинаковая:
|
|
|---|
Здесь необходимо сделать три примечания.
Примечание 1. На экзаменах не бывает задач, которые необходимо решить только с помощью векторов, для которых и
используется именно «минус единица». Поэтому для практического использования наиболее удобна формулировка, представляющая, по сути, следствие из теоремы для отрезков (это вторая формулировка, выделенная жирными буквами). Ею и ограничимся
для дальнейшего изучения теоремы Менелая, поскольку наша цель научиться применять её для решения задач.
Примечание 2. Несмотря на то, что во всех учебниках чётко оговаривается и тот случай, когда все три точки A1, B1 и C1
могут лежать на продолжениях сторон треугольника (или на прямых, содержащих стороны треугольника), на нескольких репетиторских сайтах Интернета формулируется только тот случай, когда две
точки лежат на двух сторонах, а третья — на продолжении третьей стороны. Вряд ли это можно оправдать тем, что на экзаменах встречаются только задачи первого типа и не могут
встретиться задачи, когда все эти точки лежат на продолжениях трёх сторон.
Примечание 3. Обратная теорема, т.е. условие для того, чтобы три точки лежали на одной прямой, обычно
не рассматривается вовсе, а некоторые репетиторы даже советуют (???) заниматься только прямой теоремой, и не рассматривать обратную теорему. Между тем доказательство
обратного утверждения достаточно поучительно и позволяет доказывать утверждения, похожие на то, что приведено в решении задачи 1. Опыт доказательства обратной теоремы,
несомненно, даст ощутимую пользу ученику при решении задач.
Для того, чтобы научить ученика видеть теорему Менелая в задачах и пользоваться ею при решениях
важно обратить внимание на рисунки и закономерности в записи теоремы для конкретного случая. А поскольку сама теорема в «чистом» виде, т.е. без окружения другими отрезками, сторонами
различных фигур в задачах обычно не встречается, то целесообразнее показывать теорему на конкретных задачах. А если и показывать рисунки в качестве объяснения, то делать их многовариантными.
При этом выделять одним цветом (например, красным) прямую, которая образовывается тремя точками, а синим — отрезки треугольника, участвующие в записи теоремы Менелая.
При этом те элементы, которые не участвуют, остаются чёрными:
На первый взгялд может показаться, что формулировка теоремы достаточно сложная и не всегда понятная; ведь в ней
участвуют три дроби. Действительно, если опыта у ученика недостаточно, то он легко может ошибиться в написании, и как следствие, неправильно решить задачу. И вот тут,
бывает, начинаются проблемы. Дело в том, что в учебниках обычно не акцентируется внимание на том, как «совершать обход» при написании теоремы. Ничего не говорится и о
закономерностях записи самой теоремы. Поэтому некоторые репетиторы даже рисуют различные стрелки, в каком порядке записывать формулу. И предлагают ученикам строго
следовать таким установкам. Отчасти это правильно, но куда важнее понять суть теоремы, чем чисто механически ее записывать, пользуясь «правилом обхода» и стрелками.
На самом деле, важно понять всего лишь логику «обхода», а она настолько точная, что ошибиться в написании
формулы невозможно. В обоих случаях a) и b) напишем формулу для треугольника AMC.
Для начала определяем для себя три точки — вершины треугольника. У нас это точки A, M, C. Затем определяем точки,
лежащие на пересекающей прямой (красной прямой), это — B, P, K. Начинаем «движение» с вершины треугольника, например, из точки C. Из этой точки «идём» к точке, которая образуется
пересечением, например, стороны AC и пересекающей прямой — у нас это точка K. Пишем в числитель первой дроби — СК. Дальше из точки K «идем» в оставшуюся точку на прямой AC — в точку A. В знаменатель
первой дроби пишем — KA. Так как точка A принадлежит ещё и прямой AM, то проделываем то же самое с отрезками на прямой AM. И тут опять, начинаем с вершины, далее «идём» в точку
на пересекающей прямой, после чего переходим в вершину M. «Очутившись» на прямой BC проделываем то же самое и с отрезками на этой прямой. Из M «идём» конечно же в B, после
чего возвращаемся в C. Этот «обход» можно совершать как по часовой стрелке, так и против часовой стрелки. Важно только понять правило обхода — из вершины к точке на прямой,
и от точки на прямой — к другой вершине. Примерно так обычно и объясняют правило записи произведения дробей. В итоге получается:
Обратим внимание на то, что весь «обход» отражён в записи и для удобства показан стрелками.
Однако получившуюся запись можно получить не выполняя никакого «обхода». После того, как выписаны точки — вершины
треугольника (A, M, C) и точки — лежащие на пересекающей прямой (B, P, K), записывают ещё и тройки букв, обозначающих точки, лежащие на каждой из трёх прямых. В наших случаях, это I) B, M, C;
II) A, P, M и III) A, C, K . После этого верную левую часть формулы можно написать даже не глядя на чертёж и в любом порядке. Нам достаточно из каждой тройки букв написать верные дроби, которые
подчиняются правилу — условно «средние» буквы — это точки пересекающей прямой (красные). Условно «крайние» буквы — это точки вершин треугольника (синие). При написании формулы таким способом надо следить
только за тем, чтобы любая «синяя» буква (вершина треугольника) попала бы по разу и в числитель и в знаменатель Например.
Этот метод бывает особенно полезен для случаев типа b), а также для самопроверки.
Существует несколько различных способов доказательства теоремы Менелая. Иногда доказывают с помощью подобия треугольников, для
чего из точки M (как на данном чертеже) проводят отрезок, параллельный AC. Другие проводят дополнительную прямую, не параллельную пересекающей прямой, а потом прямыми, параллельными пересекающей
словно «проецируют» все нужные отрезки на эту прямую и с помощью обобщения теоремы Фалеса (т.е. теоремы о пропорциональных отрезках) выводят формулу. Однако, пожалуй, наиболее
простой способ доказательства получается, если из точки M провести прямую, параллельную пересекающей. Докажем теорему Менелая этим способом.
Дано: Треугольник ABC. Прямая PK пересекает стороны треугольника и продолжение стороны MC в точке B.
Доказать, что выполняется равенство:
Доказательство. Проведём луч MM1, параллельно BK. Запишем отношения, в которых участвуют отрезки, которые входят в
запись формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом случае, пересекающиеся в точке C.
Перемножим левые и правые части этих уравнений:
Теорема доказана.
Аналогично доказывается теорема и для случая b}.
Из точки C проведём отрезок CC1, параллельный прямой BK. Запишем отношения, в которых участвуют отрезки,
которые входят в запись формулы теоремы Менелая. В одном случае рассмотрим прямые, пересекающиеся в точке A, а в другом случае, пересекающиеся в точке M. Так как в теореме
Фалеса ничего не говорится о расположении отрезков на двух пересекающихся прямых, то отрезки могут располагаться и по разные стороны от точки M. Поэтому
Теорема доказана.
Теперь докажем обратную теорему.
Дано:
Доказать, что точки B, P, К лежат на одной прямой.
Доказательство. Пусть прямая BP пересекает AC в некоторой точке K2, не совпадаюшей с точкой K.
Так как BP — это прямая, содержащая точку K2, то для неё справедлива только что доказанная теорема Менелая. Значит,
для нее запишем
Однако только что мы доказали, что
Отсюда следует, что Точки K и K2 совпадают, так как делят сторону AC в одном и том же отношении.
Для случая b) теорема доказывается аналогично.
Для начала вернёмся к Задаче 1 и решим её. Прочитаем ещё раз условие. Сделаем чертёж:
Дана трапеция ABCD. ST — средняя линия трапеции, т.е. одно из данных расстояний. Углы A и D в сумме составляют 90°.
Продлеваем боковые стороны AB и CD и на их пересечении получаем точку K. Соединим точку K с точкой N — серединой BC. Теперь докажем, что точка P, являющаяся серединой основания AD
также принадлежит прямой KN. Рассмотрим последовательно треугольники ABD и ACD. Две стороны каждого треугольника пересекает прямая KP. Предположим, прямая KN пересекает основание
AD в некоторой точке X. По теореме Менелая:
Так как треугольник AKD прямоугольный, то точка P, являющаяся серединой гипотенузы AD, равноудалена от A, D и K Аналогично точка N равноудалена от точек B, C и K.
Откуда одно основание равно 36, а другое равно 2.
|
Задача 2. В трапеции ABCD с основаниями AD и BC через точку A проведена прямая, которая пересекает диагональ BD в точке P и боковую сторону CD в точке N, причём BP : PD = 2 : 3, CN : ND = 2 : 5. Найдите отношение длин оснований трапеции. |
|---|
Решение. Рассмотрим треугольник BCD. Его пересекает луч AX, где X — точка пересечения этого луча с
продолжением стороны BC. По теореме Менелая:
Подставив (1) во (2) получаем:
|
Задача 3. В треугольнике ABC медиана BM и биссетриса AK пересекаются в точке O, AC : AB = k. Найдите отношение площадей треугольника AOB и четырёхугольника MOKC. |
|---|
Решение. Обозначим буквами S1, S2, S3 и S4 площади соответственно
треугольников AOB, AOM, BOK и четырёхугольника MOKC.
Так как BM — медиана, то SABM = SBMC.
Значит, S1 + S2 = S3 + S4.
Так как надо найти отношение площадей S1 и S4, поделим обе части уравнения на S4:
Подставим эти значения в формулу (1):
Из треугольника BMC при секущей AK по теореме Менелая имеем:
Из треугольника AKC при секущей BM по теореме Менелая имеем:
Все нужные отношения выражены через k и теперь можно подставить их в выражение (2):
© Репетитор по математике в Москве, Александр Анатольевич, 8-968-423-9589.
1) Задача попроще. На медиане BD треугольника ABC отмечена точка M так, что BM : MD = m : n.
Прямая AM пересекает сторону BC в точке K.
Найдите отношение BK : KC.
2) Задача посложнеее. Биссектриса угла A параллелограмма ABCD пересекает сторону ВС в точке P,
а диагональ BD — в точке T. Известно, что AB : AD = k (0 < k < 1). Найдите отношение площадей треугольника BTP и параллелограмма ABCD.
3) Задача № 26 ОГЭ. В треугольнике ABC
биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 36. Найдите стороны
треугольника ABC.
Подсказка репетитора по математике. В Интернете встречается решение такой задачи с помощью дополнительного построения и далее либо подобия,
либо нахождения площадей, и только после этого сторон треугольника. Т.е. оба этих способа требуют
дополнительного построения. Однако решение такой задачи с помощью свойства биссектрисы и теоремы
Менелая не требует никаких дополнительных построений. Оно гораздо проще и рациональнее.

Имею большой опыт работы репетитором. За два десятилетия выработаны собственные методики занятий. Окончил технический ВУЗ – Московский автомобильно-дорожный институт в 1987 г.
Еще в институте оказывал помощь однокурсникам по высшей математике. Репетиторством занимаюсь с 1998 г. За это время мною подготовлено к различным экзаменам более 200 учеников.
Специализируюсь на подготовке в лицеи и математические школы, готовлю к сдаче ОГЭ и ЕГЭ. Занимаюсь также сопровождением школьной программы — подготовкой к контрольным
и самостоятельным работам. Прививаю навыки быстрого устного счета, рассматриваю с учениками логические и нестандартные задачи, направленные на воспитание интереса к предмету,
на развитие логического мышления.