Площадь параллелограмма — одно из основных понятий геометрии‚ которое позволяет нам определить размеры этой фигуры. Параллелограмм представляет собой четырехугольник‚ у которого противоположные стороны параллельны и равны по длине.
Расчет площади параллелограмма является важной задачей при решении различных геометрических задач. Зная значения длин его сторон или высоту‚ мы можем точно определить его площадь.
В данной секции мы рассмотрим основные методы расчета площади параллелограмма и приведем примеры для более наглядного объяснения. Также будут рассмотрены свойства параллелограммов‚ которые помогут лучше понять эту фигуру и ее характеристики.
Определение площади параллелограмма
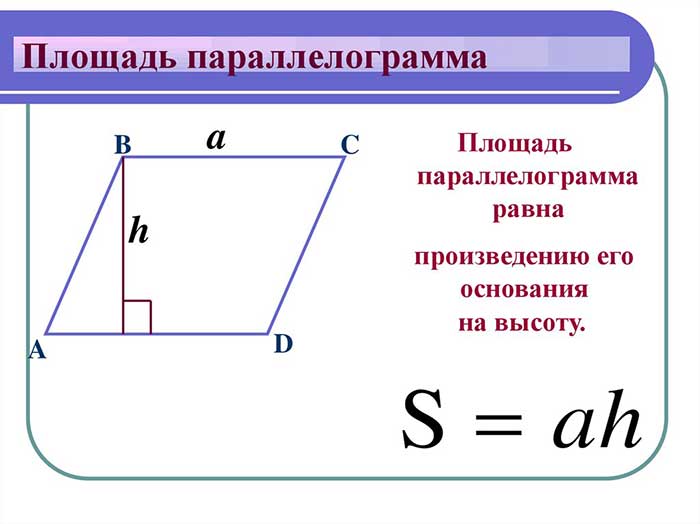
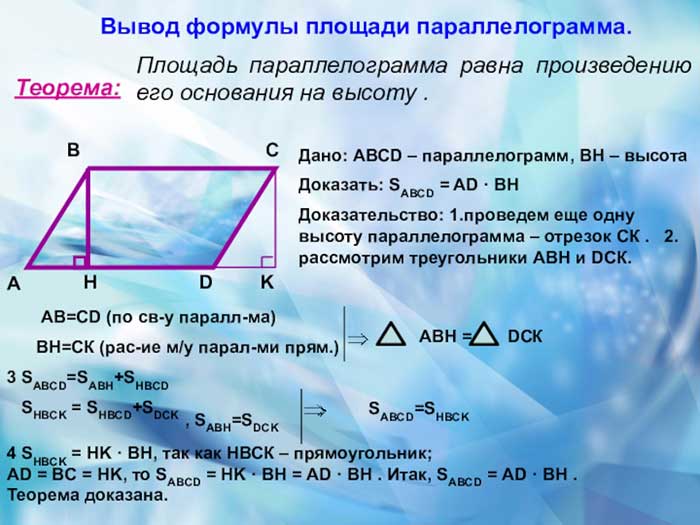
Площадь параллелограмма определяется как произведение длины одной из его сторон на высоту‚ проведенную к этой стороне.
Для удобства расчета площади‚ обычно выбирают одну из сторон параллелограмма в качестве базиса и проводят высоту‚ которая перпендикулярна базису. Длина этой высоты является высотой параллелограмма.
Формула для расчета площади параллелограмма: S = a * h‚ где S — площадь‚ a, длина базиса (стороны)‚ h — высота.
Важно отметить‚ что любая сторона и соответствующая ей принадлежащая ей высота могут быть выбраны в качестве базисной линии и соответствующей ей высоты; Результат будет одинаковый.
Формула площади параллелограмма
Формула для расчета площади параллелограмма основана на принципе умножения длины одной из его сторон на высоту‚ проведенную к этой стороне.
При выборе базисной линии и соответствующей ей высоты можно использовать следующие формулы:
- Для параллелограмма с основанием a и соответствующей ему высотой h:
Площадь S = a * h
- Для параллелограмма с двумя сторонами a и b‚ между которыми заключен угол α:
Площадь S = a * b * sin(α)
Эти формулы позволяют нам быстро и точно рассчитывать площадь параллелограмма в зависимости от заданных параметров.
Описание формулы
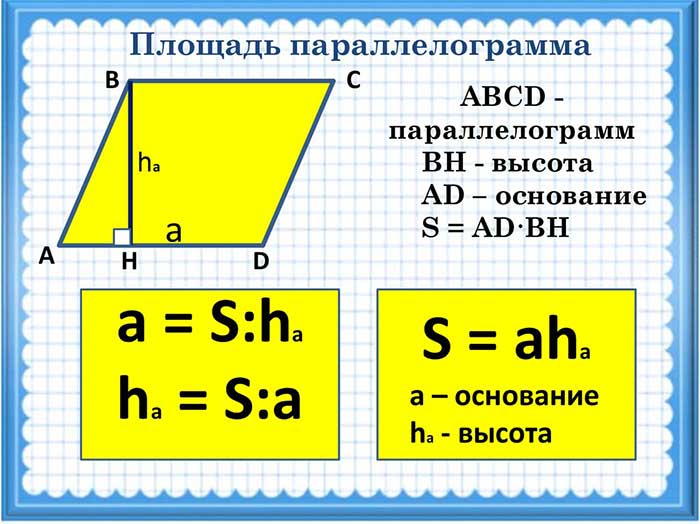
Для расчета площади параллелограмма с основанием a и соответствующей ему высотой h‚ используется простая формула: S = a * h.
Эта формула основана на принципе умножения длины одной из сторон (основания) на высоту‚ проведенную к этой стороне; Результатом будет площадь параллелограмма в единицах квадратных.
Если же известны две стороны a и b параллелограмма‚ между которыми заключен угол α‚ то для расчета площади можно использовать следующую формулу: S = a * b * sin(α);
В данной формуле sin(α) представляет собой синус угла α. Это связано с тем‚ что площадь параллелограмма определяется как произведение длин двух его сторон и синуса угла между ними.
Примеры вычисления площади параллелограмма
Давайте рассмотрим несколько примеров‚ чтобы лучше понять процесс вычисления площади параллелограмма.
Пример 1
Пусть у нас есть параллелограмм с основанием a = 5 см и соответствующей ему высотой h = 8 см. Используя формулу S = a * h‚ мы можем найти его площадь:
S = 5 см * 8 см = 40 кв.см
Пример 2
Рассмотрим параллелограмм‚ у которого сторона a = 6 м и сторона b = 4 м‚ а угол α между ними равен π/3 (60 градусов). С использованием формулы S = a * b * sin(α)‚ мы можем рассчитать его площадь:
S = (6 м) * (4 м) * sin(π/3) ≈ 24 кв.м
Таким образом‚ эти примеры демонстрируют использование различных формул для расчета площади параллелограмма в зависимости от известных параметров.
Площадь параллелограмма, важное понятие геометрии‚ которое позволяет нам определить размеры этой фигуры. Расчет площади основывается на принципе умножения длины одной из сторон на высоту‚ проведенную к этой стороне.
Мы рассмотрели различные методы расчета площади параллелограмма‚ включая использование формулы S = a * h для параллелограмма с основанием и соответствующей ему высотой‚ а также формулы S = a * b * sin(α) для параллелограмма с двумя сторонами и углом между ними.
Примеры вычисления площади помогли наглядно продемонстрировать применение этих формул в конкретных задачах.
Знание и использование этих методов расчета позволит легко определить площадь любого параллелограмма и применять его в решении геометрических задач.