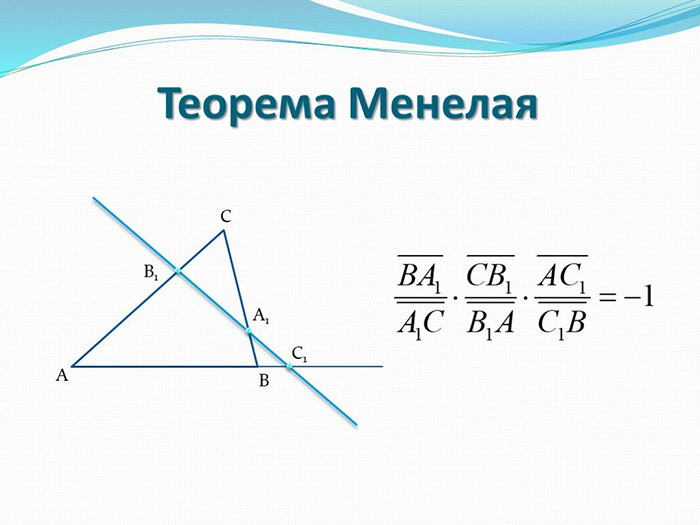
Теорема Менелая – одна из важных теорем в геометрии, которая имеет широкое применение при решении задач связанных с треугольниками․ Теорема была названа в честь французского математика Жерара Менелая, который впервые её доказал․
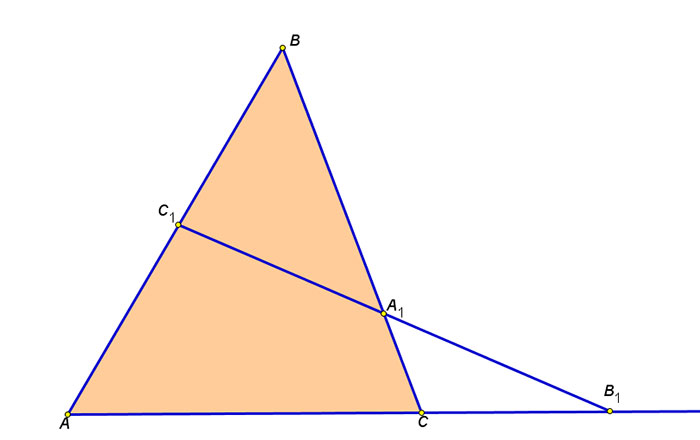
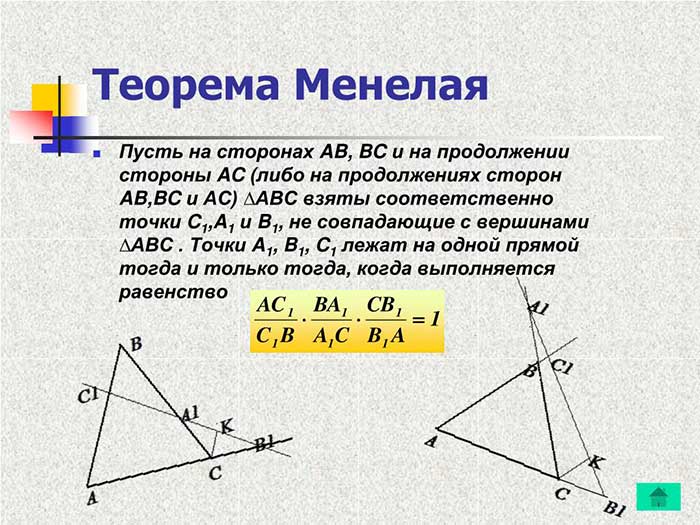
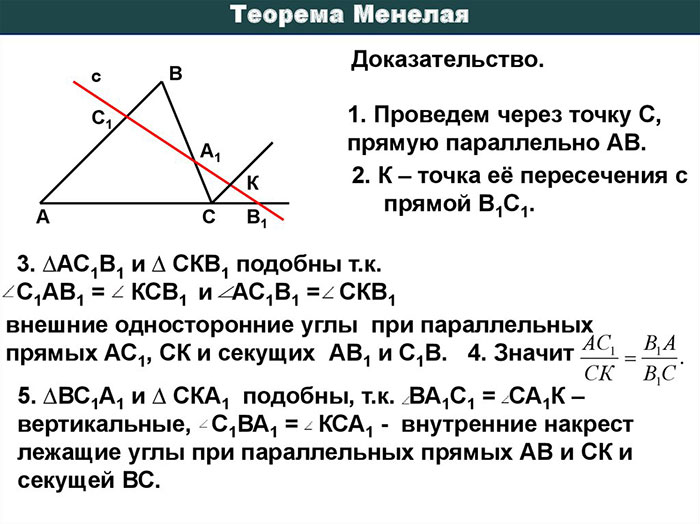
Теорема Менелая утверждает, что для трех точек A, B и C на одной прямой и произвольной точки D лежащей на этой прямой выполняется следующее равенство:
(AD/DB) * (BE/EC) * (CF/FA) = 1
где AD, DB – отрезки разделены точкой D на отрезке AB; BE, EC – отрезки разделены точкой E на отрезке BC; CF, FA – отрезки разделены точкой F на отрезке CA․
Данная формула позволяет решать множество геометрических задач: вычислять неизвестные стороны или расстояния между точками треугольника при условии известных соотношений между этими сторонами или расстояниями.
Что такое теорема Менелая?
Теорема Менелая является одним из важных результатов в геометрии, которые позволяют решать задачи связанные с треугольниками․ Она была названа в честь французского математика Жерара Менелая, который первым её доказал․
Суть теоремы заключается в следующем: для трех точек A, B и C на одной прямой и произвольной точки D лежащей на этой прямой выполняется равенство:
(AD/DB) * (BE/EC) * (CF/FA) = 1
где AD, DB – отрезки разделены точкой D на отрезке AB; BE, EC – отрезки разделены точкой E на отрезке BC; CF, FA – отрезки разделены точкой F на отрезке CA․
Эта формула позволяет решать множество геометрических задач․ Например, если известны только соотношения между сторонами или расстояниями трех точек треугольника, то можно вычислить неизвестные стороны или расстояния между точками треугольника․
Формулировка теоремы
Теорема Менелая утверждает, что для трех точек A, B и C на одной прямой и произвольной точки D лежащей на этой прямой выполняется следующее равенство:
(AD/DB) * (BE/EC) * (CF/FA) = 1
где AD, DB – отрезки разделены точкой D на отрезке AB; BE, EC – отрезки разделены точкой E на отрезке BC; CF, FA – отрезки разделены точкой F на отрезке CA․
Эта формула может быть использована для решения множества геометрических задач связанных с треугольниками․ Например, если известно соотношение между длинами сторон треугольника или расстояний до его вершин, то можно вычислить неизвестные стороны или расстояния․
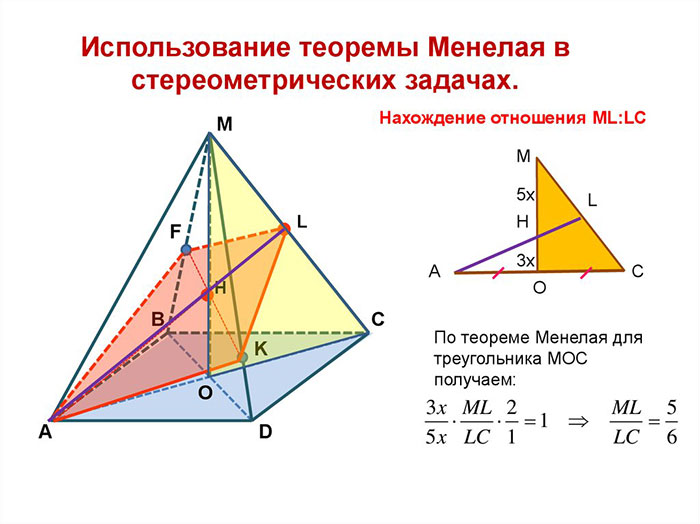
Также теорема Менелая имеет важное приложение в области физики․ Она используется при анализе равновесия систем сил и моментов с помощью векторных методов․
Описание основной формулировки теоремы Менелая
Теорема Менелая является одним из фундаментальных результатов в геометрии, которая позволяет решать разнообразные задачи, связанные с треугольниками․ Основная формулировка теоремы Менелая заключается в следующем:
Для трех точек A, B и C на одной прямой и произвольной точки D лежащей на этой прямой выполняется равенство:
(AD/DB) * (BE/EC) * (CF/FA) = 1
Здесь AD и DB представляют отрезок AB, который разделен точкой D; BE и EC – отрезок BC, разделенный точкой E; CF и FA – отрезок CA, разделенный точкой F․
Формула теоремы Манелая позволяет вычислить неизвестные стороны или расстояния между точками треугольника при условии известных соотношений между этими сторонами или расстояниями․ Также она может быть использована для анализа равновесия систем сил и моментов в физике с помощью векторных методов․
Теорема Менелая имеет широкое применение и является одним из ключевых инструментов для решения геометрических задач, связанных с треугольниками․
Теорема Менелая является важным результатом в геометрии и находит широкое применение при решении задач, связанных с треугольниками․ Она позволяет вычислять неизвестные стороны или расстояния между точками треугольника при известных соотношениях между ними․
Основная формулировка теоремы Менелая гласит: для трех точек A, B и C на одной прямой и произвольной точки D лежащей на этой прямой выполняется равенство (AD/DB) * (BE/EC) * (CF/FA) = Эта формула может быть использована для решения различных геометрических задач․
Также стоит отметить, что теорема Менелая имеет важное приложение в физике при анализе равновесия систем сил и моментов с помощью векторных методов․
В заключении можно сказать, что теорема Менелая является полезным инструментом для решения задач связанных с треугольниками и её знание может быть полезно в различных областях, где требуется работа с геометрическими объектами․