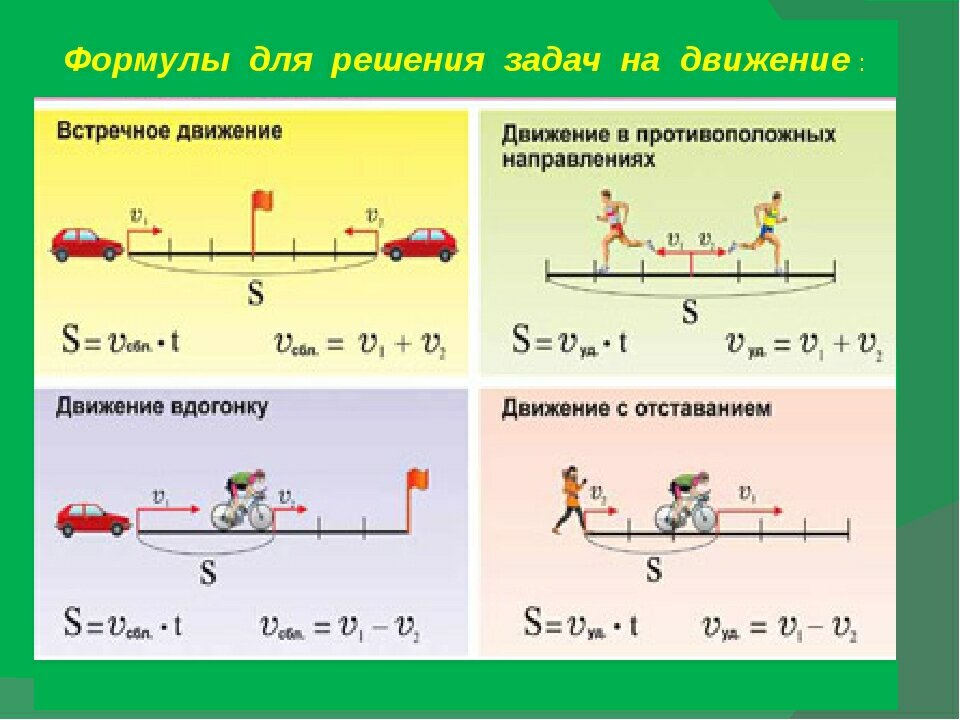
Задачи на движение
Наверное, ни одна олимпиада по математике в 5-6 классах не обходится без какой-либо задачи на движение.
Однако поскольку в отличие от некоторых других олимпиадных задач эта тема согласуется со школьной программой, то рассматривая нестандартные и олимпиадные задачи на движение
с учениками важно ориентироваться на то, что проходил ученик в школе, а что ещё нет. Это важно потому, что необходимый багаж знаний школьнику не объяснить за 5-10 минут в качестве
вводных слов — слишком большой объём теоретического материала ему надо освоить. Например, для решения некоторых задач на движение школьник должен уже уметь выполнять все действия
с дробями с разными знаменателями и иметь в этом достаточный опыт.
Лет 15 назад, когда в большинстве обычных школ изучали математику 5-6 класса по учебникам Виленкина для этих классов, то всё было просто с
рекомендациями, к какому классу относить те или иные задачи на движение. В 5-м классе проходились действия с дробями с одинаковым знаменателем, а в 6-м — приведение дробей
к одинаковому знаменателю и все действия с дробями. Но в последнее время появился целый ряд учебников, где эта традиция оказалась нарушенной. Поэтому-то так важно стало сразу же
спрашивать у ученика, по каким учебникам тот учится в школе? Действительно, бывает, что в лицеях и математических классах школьники учатся сразу по двум учебникам. Однако
если ученик в школе не проходил все действия с дробями, то задачу, где без этого не обойтись, ему вряд ли предложат и на олимпиаде. А значит, и репетитору по математике важно
ориентироваться на школьную программу ученика и не предлагать ему решать задачи, требующие от него знаний, которые он ещё не проходил в школе.
Ниже представлены задачи на движение, как не требующие от ученика умения выполнять все действия с дробями (№№ 1-9), так
и требующие (№№ 10-18), от достаточно простых, решающихся в уме, до задач повышенной сложности.
1) Два водителя выехали навстречу друг другу из Москвы и Санкт-Петербурга. Они двигались без остановок со скоростями
80 км/ч и 100 км/ч. Как далеко будут эти водители друг от друга за 1 ч до встречи?
2) Вы стоите на первом этаже шестиэтажного дома. Чтобы подняться на третий этаж этого дома, надо пройти 48 ступенек.
Сколько ступенек надо пройти, чтобы подняться на 6-й этаж этого дома? (Число ступенек между этажами одинаково).
3) Решите устно: Две ракеты летят навстречу друг другу, одна со скоростью 9000 км/ч, а другая — со скоростью 21000 км/ч. Их стартовые площадки
находятся на расстоянии 1317 км одна от другой. Какое расстояние будет между ракетами за 1 минуту до столкновения?
4) Два города, A и B, находятся на расстоянии 300 км друг от друга. Из этих городов одновременно выезжают навстречу друг другу
навстречу два мотоциклиста и мчатся, не останавливаясь, со скоростью 50 км/ч. Одновременно с первым мотоциклистом из города A вылетает шмель, пролетающий в час 100 км. Шмель опережает первого мотоциклиста, летит навстречу второму, выехавшему из B.
Встретив его, он сразу поворачивает назад, к мотоциклисту, выехавшему из A. Повстречав его, опять летит обратно навстречу мотоциклисту, выехавшему из B и так продолжал свои полёты вперёд и назад
до тех пор, пока мотоциклисты не съехались. Тогда он успокоился и сел одному мотоциклисту на куртку. Сколько километров пролетел шмель?
5) Из зоопарка на пристань, находящуюся на расстоянии 1 км, повели Слона. В этот же момент от пристани навстречу Слону выбежала Моська.
Она добежала до Слона, тявкнула на него и побежала обратно на пристань, затем повернула обратно и так бегала туда-сюда, пока Слон не пришёл на пристань. Моська двигалась в 10 раз быстрее Слона. Сколько всего км пробежала Моська?
6) Поезд длиной 1 км идет со скоростью 60 км/ч. Сколько времени потребуется поезду для прохождения тоннеля длиной в 1 км?
7) Если Аня идёт в школу пешком, а обратно едет на автобусе, то всего на дорогу она тратит полтора часа. Если же она едет на автобусе
в оба конца, то весь путь у неё занимает 30 минут. Сколько времени потратит Аня на дорогу, если и в школу и из школы она будет идти пешком?
8) Петя, проезжая в трамвае, заметил своего друга Васю, который шёл вдоль трамвайной линии в противоположную сторону.
Через 10 с трамвая остановился на остановке и Петя вышел из трамвая и пошёл догонять Васю. Через сколько секунд Петя догонит Васю, если Петя идёт в два раза быстрее Васи и в 5 раз медленнее трамвая?
9) Скорый и пассажирский поезда идут навстречу друг другу по параллельным путям со скоростями 60 км/ч и 48 км/ч. Пассажир, сидящий в пассажирском поезде, заметил,
что скорый поезд прошёл мимо него в течение 5 с. Найдите длину скорого поезда.
10) Половину пути лошадь шла порожняком со скоростью 12 км/ч. Остальной путь она шла с возом, со скоростью 4 км/ч. Какова средняя скорость лошади?
11) Автомобиль проехал от одного города до другого со скоростью 60 км/ч, а обратно — со скоростью 40 км/ч. Какова была средняя
скорость его езды?
12) Два автомобиля выезжают одновременно из Москвы в Тверь. Один едет с постоянной скоростью 100 км/ч. Другой половину пути
едет со скоростью 80 км/ч, а другую половину — со скоростью 120 км/ч. Кто быстрее приедет?
13) Вдоль беговой дорожки расставлено 12 флажков на равных расстояниях друг от друга. Старт у первого флажка. У восьмого флажка
спортсмен был через 8 секунд после начала бега. Через сколько секунд при неизменной скорости он окажется у 12-го флажка?
14) Белка за 20 минут приносит орех в гнездо. Далеко ли от орешника её гнездо, если известно, что налегке белка бежит со скоростью
5 м/с, а с орехом — 3 м/с?
15) Пассажир спускается по движущемуся эскалатору за 24 с. Если же он идет по неподвижному эскалатору с той же скоростью,
то спустится вниз за 42 с. За какое время пассажир спустится вниз, стоя на ступеньках движущегося эскалатору?
16) Пароход от Саратова до Астрахани плывёт трое суток, а назад — четверо. Сколько суток будут плыть плоты от Саратова до Астрахани (наличием шлюзов можно пренебречь).
17) Старший брат проходит путь от дома до школы за 30 минут, а младший — за 40 минут. Через сколько минут старший брат
догонит младшего, если тот вышел из дома на 5 минут раньше?
18) Первая черепаха может проползти расстояние от окна до двери за 20 минут, а вторая — за 30 минут. Однажды черепахи
одновременно направились навстречу друг другу — одна от окна, другая от двери. Через сколько минут они встретились?
19) Катя и Аня бегают по круговой дорожке длиной 400 м, при этом скорость Кати в
полтора раза больше скорости Ани. Найдите скорость Кати, если каждые 6 минут она обгоняет Аню на
круг.
20) Три бегуна – Антон, Серёжа и Толя –
участвуют в беге на 100 м. Когда Антон финишировал, Серёжа находился в 10 метрах позади него, а
когда финишировал Серёжа, Толя находился позади него в 10 метрах. На каком расстоянии друг от друга
находились Толя и Антон, когда Антон финишировал? (Предполагается, что все мальчики бегут с
постоянными, но, конечно, не равными скоростями.)
21) Папа по реке доплывает от моста до пляжа за 9 минут, а от пляжа до моста — за 12 минут. Сын же от моста до пляжа
доплывает за 12 минут. Сколько времени нужно сыну, чтобы доплыть от пляжа до моста?
Репетитор по математике в Москве, Александр Анатольевич, 8-968-423-9589, подготовка к олимпиадам 5-6 классов

Имею большой опыт работы репетитором. За два десятилетия выработаны собственные методики занятий. Окончил технический ВУЗ – Московский автомобильно-дорожный институт в 1987 г.
Еще в институте оказывал помощь однокурсникам по высшей математике. Репетиторством занимаюсь с 1998 г. За это время мною подготовлено к различным экзаменам более 200 учеников.
Специализируюсь на подготовке в лицеи и математические школы, готовлю к сдаче ОГЭ и ЕГЭ. Занимаюсь также сопровождением школьной программы — подготовкой к контрольным
и самостоятельным работам. Прививаю навыки быстрого устного счета, рассматриваю с учениками логические и нестандартные задачи, направленные на воспитание интереса к предмету,
на развитие логического мышления.