Помощь в подготовке к урокам, контрольным, ЕГЭ
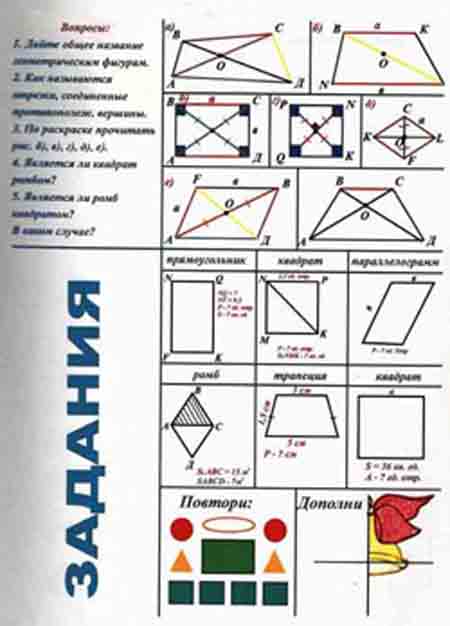
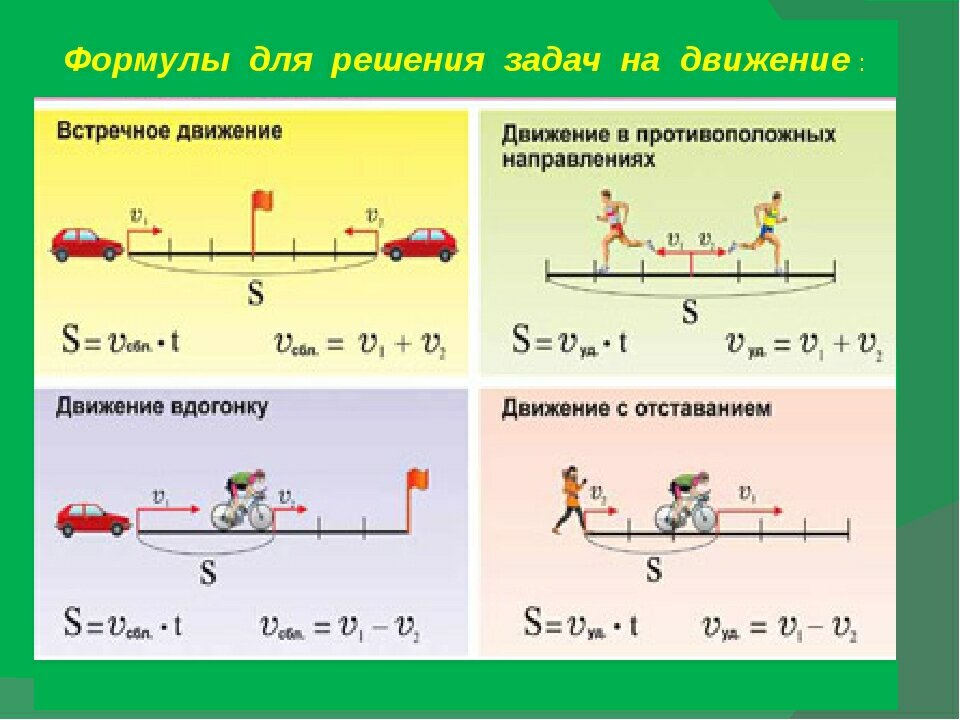
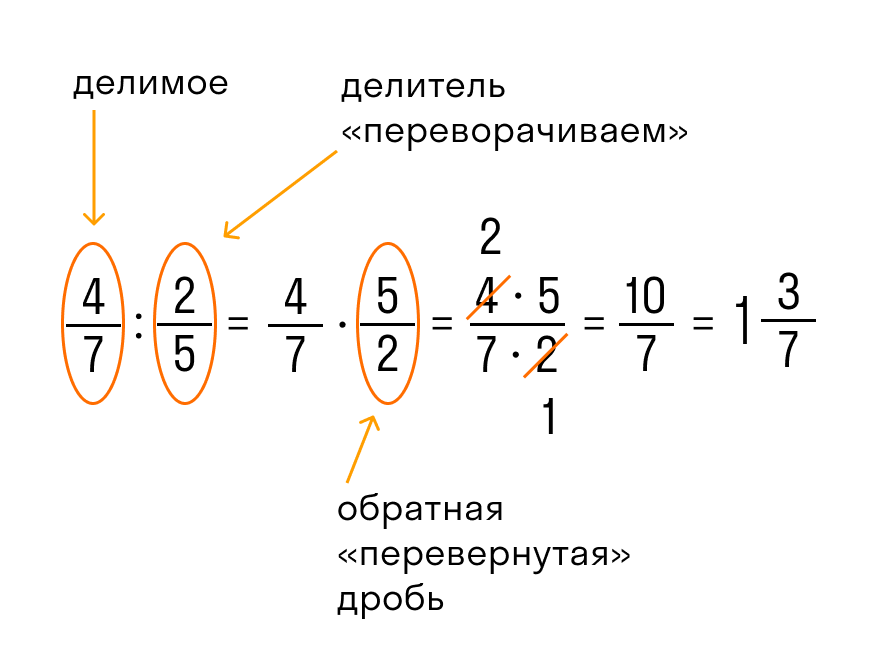А знаете ли вы элементарную математику? Дорогие друзья! Многолетний опыт опыт репетитора-преподавателя по математике позволяет мне сформулировать основную проблeму, с которой ежедневно сталкиваются дети, изучающие математику в школе, разрешить которую и призван репетитор-профессионал. Проблема, на мой взгляд, заключается в том, что изучение математики сводится к запоминанию нескольких правил действия над числами и выражениями, а также…
Нестандартные геометрические задачи Несмотря на то, что курс геометрии начинается в школе в 7-м классе, различного рода геометрические задачи, причём, зачастую достаточно оригинальные, требующие нестандартных методов решения, которые в школе не изучаются, встречаются на олимпиадах 5-6 классов, а также предлагаются на вступительных экзаменах в 5-й или 6-й класс лицеев и гимназий. Поэтому бывает полезно…
Круги Эйлера – это важный инструмент в теории графов, который позволяет анализировать связность и структуру графа. Они названы в честь знаменитого швейцарского математика Леонарда Эйлера, который первым исследовал эту концепцию. Введение в понятие кругов Эйлера начинается с определения самого графа. Граф – это математическая абстракция, представляющая собой множество вершин, соединенных ребрами. Вершины обозначают объекты или…
Задачи на движение Наверное, ни одна олимпиада по математике в 5-6 классах не обходится без какой-либо задачи на движение. Однако поскольку в отличие от некоторых других олимпиадных задач эта тема согласуется со школьной программой, то рассматривая нестандартные и олимпиадные задачи на движение с учениками важно ориентироваться на то, что проходил ученик в школе, а…
Дроби Одной из наиболее изучаемых в 5-6 классах является тема «Дроби». И хотя на олимпиадах по математике в последнее время всё чаще и чаще встречаются задачи на логику, и всё меньше и меньше на дроби, такого рода задачи также важно уметь решать. Ниже я привожу задачи на дроби, которые обычно предлагаю решить моим ученикам,…
Принцип Дирихле Немного теории Пожалуй, самыми типичными для математических олимпиад 5-6 класса являются задачи на принцип Дирихле. Для того, чтобы стало сразу понятно, о чем речь, рассмотрим задачу из олимпиады для 5-го класса: Пример 1. Каждая сторона куба разделена на четыре квадрата. Квадраты каждой стороны заполняют единицами, причём на каждой стороне помещают разное количество…
Признаки делимости на 7, 11, 13 и более сложные задачи на делимость Страница находится в стадии подготовки… Имею большой опыт работы репетитором. За два десятилетия выработаны собственные методики занятий. Окончил технический ВУЗ – Московский автомобильно-дорожный институт в 1987 г. Еще в институте оказывал помощь однокурсникам по высшей математике. Репетиторством занимаюсь с 1998 г. За…
Делимость Задачи, в которых используются признаки делимости, часто встречаются на олимпиадах и нередко вызывают у школьников затруднения. Это во многом связано с тем, что в школьной программе признакам делимости отводится слишком мало часов, да и задач на тему делимости в учебниках довольно мало. В результате у учеников часто нет опыта в том, где эти…
Задачи на числа На этой странице собраны различные задачи на числа, встречавшиеся на различных математических олимпиадах, — такие, которые или не попали в другие темы (например, в темы «Чётность», «Принцип Дирихле», «Дроби» и др.) или же основаны на какой-либо оригинальной идее или сразу на нескольких. Задачи 1) Найдите четыре последовательных натуральных числа, если известно,…
Чётность и нечётность. Формула чётного числа. Формула нечётного числа Немного теории Среди олимпиадных задач для 5-6 классов обычно особую группу составляют такие, где требуется использовать свойства чётности (нечётности) чисел. Простые и очевидные сами по себе эти свойства легко запоминаются или выводятся, и часто у школьников не возникает каких-либо сложностей при их изучении. Но порой применить…