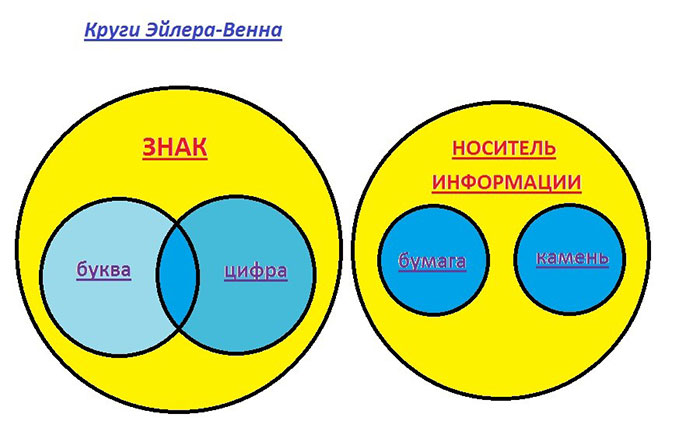
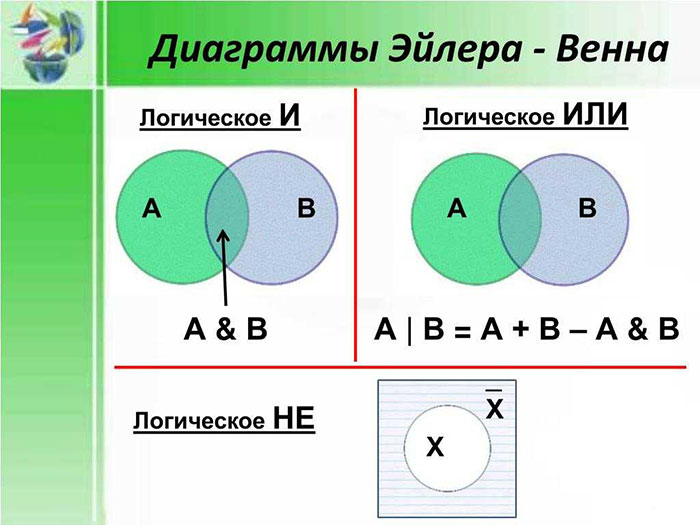
Круги Эйлера – это важный инструмент в теории графов, который позволяет анализировать связность и структуру графа. Они названы в честь знаменитого швейцарского математика Леонарда Эйлера, который первым исследовал эту концепцию.
Введение в понятие кругов Эйлера начинается с определения самого графа. Граф – это математическая абстракция, представляющая собой множество вершин, соединенных ребрами. Вершины обозначают объекты или сущности, а ребра – связи или отношения между ними.
Круг Эйлера представляет собой циклическую последовательность ребер графа, проходящую через каждую вершину только один раз и заканчивающуюся в той же самой вершине. Каждый круг является замкнутым путем без повторений вершин.
Суть кругов Эйлера заключается в том, что они помогают определить связность графа и его эйлеровость. Связность графа означает, что существует путь между любыми двумя вершинами. Эйлеровость – это свойство графа иметь эйлеров круг, который проходит через каждое ребро только один раз.
Круги Эйлера имеют широкое применение в различных областях, таких как транспортная логистика, сетевой анализ и компьютерные науки. Они помогают оптимизировать пути перемещения и выявлять структуру сложных систем.
Круги Эйлера были открыты и впервые описаны швейцарским математиком Леонардом Эйлером в XVIII веке. В своих работах он занимался изучением проблемы существования пути, проходящего через каждое ребро графа только один раз.
Первое упоминание о кругах Эйлера появилось в его статье «Solutio problematis ad geometriam situs pertinentis» (Решение задачи, касающейся геометрии местности), опубликованной в 1736 году. В этой статье он рассмотрел известную задачу семи Кёнигсбергских мостов – как найти путь, который проходит через каждый из этих мостов только один раз.
Эйлер предложил новый подход к решению этой задачи⁚ он абстрагировал её от конкретных деталей города и представил её как абстрактный граф. Затем он доказал, что для существования такого пути необходимо и достаточно чтобы все вершины имели четную степень.
В своих последующих работах Эйлер продолжал исследовать круги Эйлера и развивать теорию графов. Он внес значительный вклад в области комбинаторики и математической логики, открыв новые подходы к решению сложных задач.
Сегодня круги Эйлера являются одной из основных концепций теории графов и находят применение во многих областях, от компьютерных наук до сетевого анализа.
Круги Эйлера находят широкое применение в реальной жизни и помогают решать различные задачи. Вот несколько примеров:
- Транспортная логистика. Круги Эйлера используются для оптимизации путей перемещения грузов или транспорта. Например, при планировании маршрутов доставки товаров по разным точкам города или страны, круги Эйлера помогают найти самый эффективный маршрут, проходящий через каждую точку только один раз.
- Сетевой анализ. Круги Эйлера применяются для изучения структуры сложных сетей, таких как социальные сети, телекоммуникационные сети или интернет-серверы. Они позволяют выявить ключевые узлы и связности в сети, что полезно для определения наилучших стратегий распределения ресурсов или обнаружения уязвимостей системы.
- Графический дизайн. Круги Эйлера используются в дизайне информационных графиков и диаграмм. Они помогают визуализировать связи между различными категориями или элементами данных, обеспечивая легкое восприятие и анализ информации.
Это лишь некоторые примеры применения кругов Эйлера в реальной жизни. Их универсальность и эффективность делают этот инструмент неотъемлемой частью различных областей знания и практических приложений.
Круги Эйлера играют важную роль в науке и технологиях, применяясь для решения различных задач в следующих областях:
- Теория графов. Круги Эйлера являются одной из основных концепций теории графов. Они позволяют анализировать связность и структуру графа, определять эйлеровость и гамильтоновость графа, а также решать другие комбинаторные задачи.
- Компьютерные науки. Круги Эйлера используются для оптимизации алгоритмов и программирования. Например, они помогают ускорить поиск данных в базах данных или определить порядок выполнения операций в компьютерных сетях.
- Маркетинг и социальная аналитика. Круги Эйлера применяются для изучения потребительских предпочтений, поведения пользователей или социального взаимодействия. Они помогают выделить ключевые факторы или тренды, которые могут быть использованы для разработки маркетинговых стратегий или прогнозирования поведения аудитории.
Это лишь некоторые области, где круги Эйлера играют важную роль и применяются для решения различных задач. Их значительный вклад в науку и технологии подтверждает их универсальность и практическую ценность.