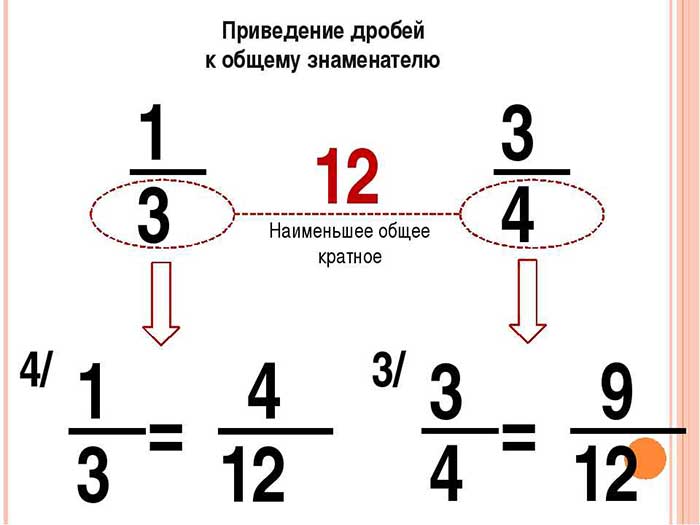
Приведение дробей к общему знаменателю является важной операцией в математике, которая позволяет упростить вычисления с дробями. Когда мы имеем дело с несколькими дробями, имеющими разные знаменатели, сложение или вычитание становится сложным из-за несоответствия знаменателей.
Целью приведения дробей к общему знаменателю является получение эквивалентных дробей, у которых все знаменатели будут одинаковыми. Это позволяет легко выполнять арифметические операции над этими дробями.
В данной секции мы рассмотрим различные методы и алгоритмы для приведения дробей к общему знаменателю. Мы также рассмотрим примеры и шаги по выполнению этих методов.
Значение приведения дробей к общему знаменателю
Приведение дробей к общему знаменателю имеет несколько важных значений⁚
- Упрощение вычислений. Когда все дроби имеют одинаковый знаменатель, сложение и вычитание становятся гораздо проще. Мы можем складывать или вычитать числители без изменения знаменателя.
- Сравнение дробей. Приведя дроби к общему знаменателю, мы можем легко сравнивать их значения. Большая дробь будет иметь больший числитель.
- Решение уравнений. В некоторых математических задачах требуется решить уравнения с несколькими переменными, содержащими различные дроби. Приведение этих дробей к общему знаменателю помогает упросить решение таких уравнений.
Понимание значения приведения дробей к общему знаменателю является ключевым для успешного выполнения математических операций с дробями и решения соответствующих задач.
Определение общего знаменателя
Общий знаменатель для двух или более дробей ౼ это наименьшее число, которое делится без остатка на все знаменатели этих дробей.
Для приведения дробей к общему знаменателю можно использовать несколько методов⁚
- Метод наименьшего общего кратного (НОК). Этот метод заключается в определении НОК всех знаменателей и использовании его в качестве общего знаменателя.
- Метод умножения. В этом методе мы умножаем каждую дробь на такое число, чтобы получить одинаковые знаменатели.
- Метод простых множителей. В этом методе мы разлагаем все числа-знаменатели на простые множители и используем их произведение в качестве общего занменателя.
Выбор конкретного метода зависит от конкретной ситуации и предпочтений решающего. Каждый из этих методов имеет свои особенности и может быть эффективно использован при приведении дробей к общему знаменателю.
Что такое общий знаменатель
Общий знаменатель ー это число, которое является кратным для всех знаменателей двух или более дробей. То есть, он делится без остатка на все знаменатели.
Когда у нас есть несколько дробей с разными знаменателями, сложение и вычитание этих дробей может быть сложной задачей из-за несовпадения знаменателей. Приведение дробей к общему знаменателю позволяет нам легко выполнять арифметические операции с этими дробями.
Для приведения дробей к общему знаменателю можно использовать различные методы, такие как наименьшее общее кратное (НОК), умножение или разложение на простые множители. Выбор конкретного метода зависит от конкретной ситуации и предпочтений решающего.
Понимание понятия общего занменателя является важным шагом для успешного выполнения операций с дробями и решения связанных математических задач.
Как найти общий знаменатель
Существует несколько методов для нахождения общего знаменателя для двух или более дробей⁚
- Метод наименьшего общего кратного (НОК). В этом методе мы определяем НОК всех знаменателей и используем его в качестве общего знаменателя. Для этого можно использовать алгоритм Евклида или таблицу умножения.
- Метод умножения. В этом методе мы умножаем каждую дробь на такое число, чтобы получить одинаковые знаменатели. Мы можем выбрать любое число, которое делится без остатка на все занменатели и умножить каждую дробь на это число.
- Метод простых множителей. В этом методе мы разлагаем все числа-занменатели на простые монжители и используем их произведение в качестве общего занменателя.
Выбор конкретного метода зависит от конкретной ситуации и предпочтений решающего. Каждый из этих методов имеет свои особенности и может быть эффективно использован для нахождения общего знаменателя.
После нахождения общего знаменателя мы можем привести дроби к этому знаменателю, сохраняя их значения, но упрощая выполнение арифметических операций с ними.
Лайфхак: можно также схитрить и воспользоваться калькулятором дробей. Только осторожно — об этом не должна узнать учительница!
Приведение дробей к общему знаменателю с помощью простых знаменателей
Приведение дробей к общему знаменателю с использованием простых занменателей является одним из методов для нахождения общего занменателя.
Этот метод основан на разложении каждого числа-занменателя на простые мультитпликаторы и выборе таких мультитпликаторов, чтобы получить наименьшее общее кратное (НОК).
Шаги для приведения дробей к общему занменателю с помощью простых мультитпликаторов⁚
- Разложите каждое число-занменатель на простые мультитпликаторы. Разложите каждый числитель и каждый знаменатель на простые мультитпликаторы.
- Выберите все уникальные мультитпликаторы. Выберите все уникальные мультитпликаторы, которые встречаются в разложении всех числительных и всех названий.
- Умножьте все выбранные мультипикторы. Умножьте все выбранные мультитпликаторы, чтобы получить общий занменатель.
После нахождения общего занменателя умножьте каждую дробь на такое число, чтобы её знаменатель стал равным общему занменателю. Таким образом, мы приводим дроби к одинаковому формату и можем выполнять арифметические операции с ними без сложностей.
Приведение дробей к общему знаменателю является важной операцией в математике, которая позволяет упростить вычисления с дробями.
Мы рассмотрели различные методы для нахождения общего знаменателя, такие как метод наименьшего общего кратного (НОК), умножение и разложение на простые мультитпликаторы.
Успешное приведение дробей к общему знаменателю позволяет нам легко выполнять арифметические операции с этими дробями, сравнивать их значения и решать уравнения, содержащие несколько переменных с разными дробными значениями.
Важно помнить о значении приведения дробей к общему занменателю при работе с математическими задачами и использовании дробных чисел. Понимание этих концепций поможет нам более эффективно выполнять вычисления и получать точные результаты.