Введение
Площадь треугольника ー одна из основных характеристик этой геометрической фигуры. Расчет площади треугольника имеет важное значение как в математике‚ так и в различных областях науки и техники.
В данной секции мы рассмотрим основные методы расчета площади треугольника‚ а также приведем примеры и задачи для более наглядного представления.
Для начала необходимо установить базовые определения: треугольник ー это многоугольник с тремя сторонами и тремя углами. При расчете его площади используются различные формулы‚ которые зависят от доступной информации о фигуре.
Основными методами вычисления площади треугольника являются:
- Метод полупериметра: использует полупериметр (сумму всех сторон‚ деленную на 2) и длины сторон треугольника;
- Метод Герона: основан на формуле Герона‚ которая связывает длины сторон треугольника и его площадь;
- Метод векторного произведения: использует векторное произведение двух сторон треугольника.
В дальнейшем мы рассмотрим каждый из этих методов более подробно‚ а также приведем примеры и задачи для закрепления материала. Также можно разгадать загадки про теругольник, которые помогуть запомнить эту фигуру. Приступим к изучению расчета площади треугольника!
Определение площади треугольника
Площадь треугольника ー это мера его поверхности‚ выраженная в квадратных единицах. Она позволяет нам оценить‚ насколько большой или маленькой является данная геометрическая фигура.
Существует несколько способов определения площади треугольника. В основе всех этих методов лежит принцип разбиения треугольника на более простые фигуры (например‚ на параллелограммы или прямоугольники)‚ для которых формулы расчета площади уже известны.
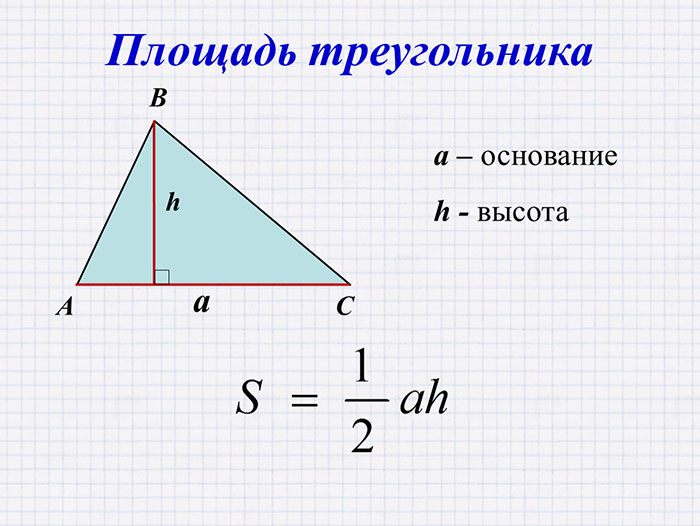
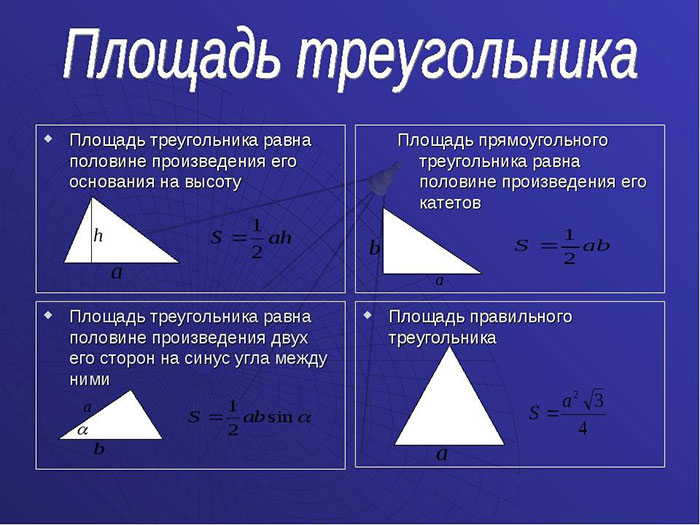
Одним из самых распространенных методов является использование высоты треугольника. Высота ー это отрезок‚ проведенный из вершины перпендикулярно основанию (стороне) треугольника. Площадь такого треугольника можно найти как произведение половины длины основания и соответствующей высоты:
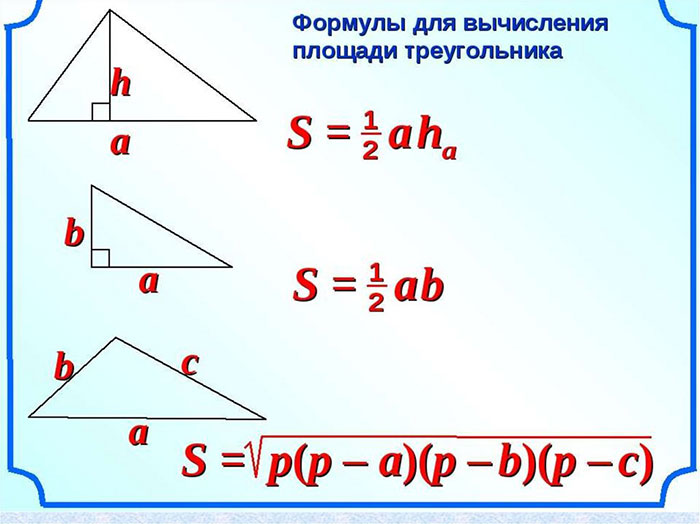
S = * a * h
где S ー площадь треугольника‚ a ー длина основания‚ h ー высота.
Важно отметить‚ что основание и высота треугольника должны быть взаимно перпендикулярными. Если такого условия нет‚ то необходимо применять другие методы расчета площади.
Далее мы рассмотрим и другие способы определения площади треугольника и детально разберем каждый из них. Продолжаем изучение!
Формула для вычисления площади треугольника
Существует несколько формул‚ которые позволяют вычислить площадь треугольника в зависимости от доступной информации о фигуре.
Метод полупериметра
Один из наиболее простых способов расчета площади треугольника ー это использование метода полупериметра (полусуммы всех сторон). Для этого нужно знать длины всех сторон треугольника: a‚ b и c. По формуле:
S = √(s * (s ⎻ a) * (s ー b) * (s ⎻ c))
где S ⎻ площадь треугольника‚ s = (a b c) / 2 ー полупериметр.
Метод Герона
Метод Герона основан на том же принципе разбиения треугольника на более простые фигуры с известными формулами для расчета их площадей. Для его использования необходимо знать только длины сторон треугольника: a‚ b и c. Формула выглядит следующим образом:
S = √(s * (s ー a) * (s ⎻ b) * (s ー c))
где S ⎻ площадь треугольника‚ s = (a b c) / 2 ⎻ полупериметр.
Метод векторного произведения
Метод векторного произведения использует математическую операцию векторного произведения для расчета площади треугольника. Для его применения необходимо знать координаты вершин треугольника: A(x1‚ y1)‚ B(x2‚ y2) и C(x3‚ y3). Формула выглядит следующим образом:
S = * |(x1*(y2-y3) x2*(y3-y1) x3*(y1-y2))|
где S ー площадь треугольника.
В зависимости от доступной информации о фигуре можно выбрать наиболее подходящий метод для расчета площади треугольника. В дальнейшем мы рассмотрим каждый из этих методов более подробно и приведем примеры для наглядности.
Определение основы и высоты треугольника
Основа и высота треугольника являются важными понятиями при расчете его площади. Они определяются отношением к одной из сторон треугольника и играют ключевую роль в различных методах расчета.
Основой треугольника называется одна из его сторон‚ на которую опускается перпендикуляр (высота). Выбор основы может быть произвольным ⎻ любая из сторон может считаться основой‚ а остальные две ⎻ боковыми сторонами.
Высотой треугольника называется отрезок‚ проведенный из вершины перпендикулярно выбранной основе. Он соединяет вершину с противоположной точкой на основании.
Важно заметить‚ что для правильного расчета площади треугольника необходимо использовать основу и высоту‚ которые взаимно перпендикулярны друг другу. Если такого условия нет‚ то следует применять другие методы для определения площади.
При использовании формулы для вычисления площади треугольника через основу и высоту‚ нужно учитывать следующее:
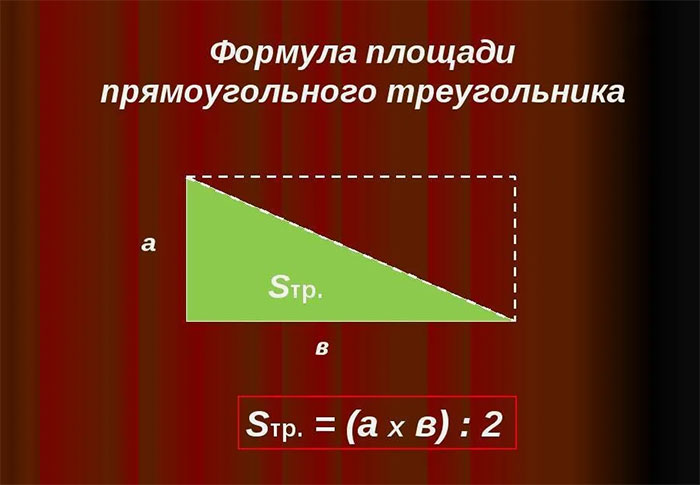
S = * a * h
где S ⎻ площадь треугольника‚ a ー длина основы‚ h ー высота.
Определение основы и высоты треугольника является важным шагом при расчете его площади. В следующих разделах мы рассмотрим конкретные методы для определения этих параметров и приведем примеры для лучшего понимания.
Расчет площади треугольника ⎻ важный аспект геометрии и науки‚ который имеет широкое применение в различных областях. На протяжении данного руководства мы рассмотрели основные методы для определения площади треугольника и изучили их формулы.
Метод полупериметра‚ метод Герона и метод векторного произведения ⎻ каждый из них имеет свои особенности и условия применимости. Выбор конкретного метода зависит от доступной информации о фигуре (длины сторон или координаты вершин) и способности использовать соответствующие формулы.
Также мы обратили внимание на определение основы и высоты треугольника‚ которые играют ключевую роль при расчете его площади. Важно помнить‚ что основа должна быть перпендикулярна высоте для правильного использования формулы S = * a * h.
Надежное понимание этих концепций поможет не только при выполнении задач по геометрии‚ но также будет полезно в инженерии‚ архитектуре и других областях‚ где требуется работа с треугольниками и расчет площадей.
Мы надеемся‚ что данное руководство помогло вам лучше разобраться в теме площади треугольника и углубить свои знания. Практикуйтесь в использовании методов расчета и не стесняйтесь задавать вопросы ー это поможет укрепить вашу экспертизу в этой области.
Удачи в изучении геометрии и успешного применения полученных знаний!