В 6-м классе, например, по учебнику Виленкина проходится пропорция. Опыт показывает, что школьники неплохо справляются с задачами на пропорцию, считая её достаточно
лёгкой темой. Более того, нередко задачи на проценты в старших классах школьники решают с помощью пропорции, забывая о том, что проценты проходятся в 5-м классе по тому же учебнику
Виленкина, а пропорция проходится в 6-м. Из чего следует вывод, что задачи на проценты можно решать, не применяя пропорцию. Однако это совсем другой вопрос. В рамках этой
статьи обратимся к пропорции и, главным образом к нестандартным задачам на пропорциональную зависимость. И пусть в обычной школе они, как правило, не проходятся, но
опыт показывает, что такие задачи вполне могут встретиться при поступлении в математические лицеи, а также на олимпиадах.
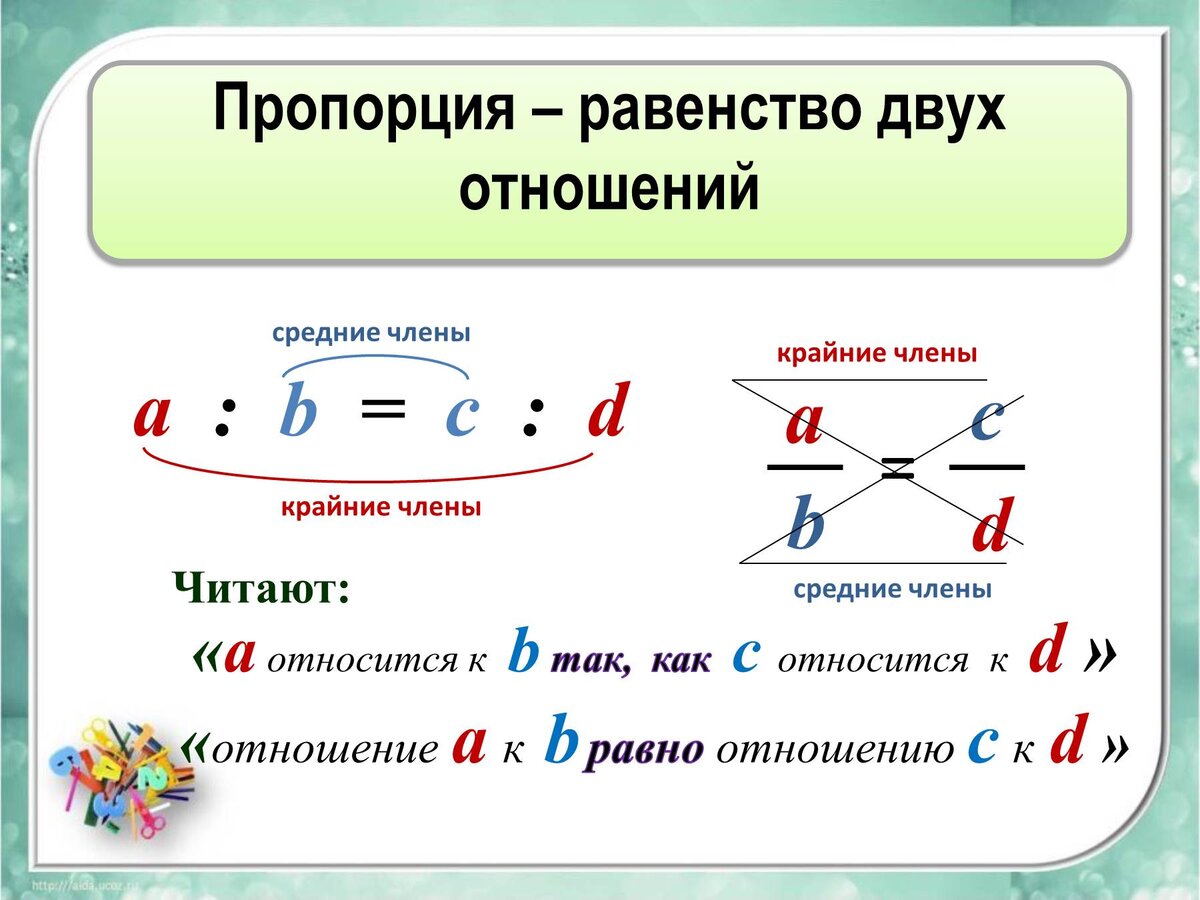
Для начала повторим теорию. Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным. Пропорция – это равенство
двух отношений. Отношение – это частное двух чисел. Отношение показывает, во сколько раз одно число больше другого
или какую часть одно число составляет от другого. Полезно напомнить и основное свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних.
Не буду останавливаться на задачах из школьного учебника, а сразу перейду к нестандартным задачам.
|
Задача 1. Поп нанял работника Балду на год, обещал ему 120 рублей и красный кафтан. Однако, проработав 7 месяцев, Балда стал просить у попа расчет и получил за работу 50 рублей и красный кафтан. Сколько стоит кафтан у Балды? |
|---|
Безусловно, эту задачу можно решить и по-другому, не прибегая к уравнению и пропорции, однако можно и пропорцией, поскольку пропорция здесь напрашивается.
Решение. Пусть x – цена кафтана. Тогда за 12 месяцев Балда мог получить 120 руб. и кафтан, т.е. 120 + x. Но за 7 месяцев он получил 50 + x.
Запишем в привычном для шестиклассника виде:
Помня о том, что по учебнику Виленкина такие уравнения (когда переменная и справа и слева от знака равенства) проходят в самом конце 6-го класса, а пропорцию примерно
в середине учебного года, применим Метод весов и вычтем 7x из обеих частей уравнения:
Таким образом, кафтан у Балды стоил 48 руб.
Куда сложнее школьникам представляются задачи на пропорциональную зависимость трёх и более величин. Причем настолько, что когда в 7 классе в учебнике геометрии (например, в учебнике Погорелова)
встречается задача, где в условии говорится, что углы треугольника пропорциональны числам 2, 3, 4 (т.е. относятся как 2:3:4), некоторые ученики приходят в замешательство и
утверждают, что не понимают условие. Действительно, в учебнике Виленкина ничего об этом не сказано. На это обстоятельство несогласованности учебников вполне можно обратить
внимание авторов-составителей новых учебников, однако наша цель рассмотреть решения нестандартных задач, так или иначе связанных с пропорциональностью.
В давние времена математика имела куда большее практическое применение, чем она имеет сейчас. И потому курс математики – тогда предмет назывался арифметикой – отвечал
насущным задачам того времени. Детей учили пропорциональному делению прибыли, наследства и т.п., и такие задачи встречались в любой книге по арифметике. В советское время такого
рода задачи исключили из школьной программы по понятным причинам, а вместе с ними и достаточно простые задачи на пропорциональное деление. Однако такого рода задачи порой
встречаются и в старых учебниках, вроде «Геометрии» Погорелова (учебник появился в 1970-х годах) или сборника задач п/р Сканави для поступающих во ВТУЗы и др. В последнее время задачи на
пропорциональное деление стали встречаться в некоторых сборниках по занимательной, нестандартной и олимпиадной математике. Рассмотрим задачу такого плана:
|
Задача 2. Три предпринимателя — Давыдов, Петров и Максимов вложили в совместную организацию предприятия по производству специальной дачной мебели деньги. Первый вложил 60 тыс. руб., второй — 90 тыс. руб., а третий — 150 тыс. руб. Они получили прибыль в размере 117 тыс. руб. Сколько денег из прибыли получит каждый из предпринимателей при условии распределения ее пропорционально их вкладам? |
|---|
Решение. Найдём, каким числам пропорциональны вклады предпринимателей. Все числа запишем в тыс. руб.
60 : 90 : 150, т.е. 2 : 3 : 5.
Исходя из этого, можно записать, что 2x + 3x + 5x = 117, где 2x — часть прибыли, которую должен получить Давыдов, 3x – часть прибыли, которую должен получить Петров,
5x — часть прибыли, которую должен получить Максимов, исходя из пропорциональности вкладов. Отсюда x = 11,7 тыс. руб., т.е. Давыдов получит 23,4 тыс. руб., Петров – 35,1 тыс. руб.,
а Максимов – 58,5 тыс. руб.
Задачу можно решить и чуть-чуть по-другому:
1) 60 + 90 + 150 = 300 тыс. руб.
2) 117 : 300 x 60 = 23,4 тыс. руб.
3) 117 : 300 x 90 = 35,1 тыс. руб.
4) 117 : 300 x 150 = 58,5 тыс. руб.
Ответ: 23, 4 тыс. руб., 35,1 тыс., руб., 58,5 тыс. руб.
Существуют и более сложные старинные задачи на дележ прибыли. Однако поскольку для их решения требуется знание квадратного уравнения, которое проходится в
8-м классе, а эта статья адресована пятиклассникам и шестиклассникам, поступающим в математические лицеи, то позволю себе их не рассматривать на этой странице, а перейти сразу
к задачам на пропорциональность трёх и более величин. Пожалуй, самая известная задача на эту тему следующая:
| Задача 3. Три курицы за 3 дня снесли три яйца. Сколько яиц снесут 12 кур за 12 дней? |
|---|
Для того, чтобы ученик лучше понял условие, уместно одновременно рассмотреть и несколько другую задачу:
| Задача 4. Пять землекопов за 5 часов выкапывают 5 метров канавы. Сколько потребуется землекопов, чтобы за 100 часов выкопать 100 м канавы? |
|---|
Каким же удивлением для ученика, впервые знакомящегося с такого рода задачами, становится тот факт, что и в Задаче № 3, и в Задаче № 4, казалось бы «очевидные» ответы
– 12 в первой и 100 во второй – не являются правильными! В задаче № 3 правильный ответ – 48, а в задаче № 4 – правильный ответ – 5. Если дней в 4 раза больше, а кур также
в 4 раза больше, то яиц они снесут 3 х 4 х 4 = 48. Что касается второй задачи, то решение еще проще. Так как за 5 часов землекопы выкапывают 5 метров канавы, то за 1 час – 1 метр
канавы. И значит, за 100 часов 100 м канавы выкопают те же 5 землекопов.
Рассмотрим задачу, предлагающуюся для поступающих в 6-й класс лицея «Вторая школа»:
| Задача 5. 2 робота за 3 часа собирают 1 компьютер. Сколько компьютеров соберут 10 роботов за 12 часов? |
|---|
Иногда условия таких задач выписывают примерно также как обычную пропорцию и делают стрелочки. Например:
Между тем, в обычной программе таких задач нет, а ученики, поступающие в лицеи, стремятся рассуждать логически, невзирая на требования к оформлению
решений задач на пропорции в школе, то какие-либо «дежурные» схемы, здесь обычно не применяются. Главное уметь задавать вопросы и отвечать на них, решая задачу поэтапно.
Например, такие:
Решение. Если 2 робота за 3 часа собирают 1 компьютер, то сколько компьютеров соберут те же два робота за 12 часов? Если у двух роботов будет
времени в 4 раза больше, то и соберут они в 4 раза больше компьютеров, т.е. 4 компьютера. То есть 2 робота за 12 часов собирают 4 компьютера. Далее. Если роботов будет 10,
то сколько компьютеров они соберут за 12 часов? Так как роботов будет в 5 раз больше, то и соберут они за 12 часов в 5 раз больше компьютеров. То есть 10 роботов за 12 часов
соберут 20 компьютеров.
| Задача 6. 3 маляра за 5 дней могут покрасить 60 окон. Сколько окон покрасят 5 маляров за 4 дня? |
|---|
Решение. 1 маляр за 5 дней может покрасить 20 окон (60 : 3), а за один день он покрасит 4 окна (20 : 5). Значит, за 4 дня он покрасит
16 окон (4 x 4). А если таких маляров будет 5, то окон будет покрашено 5 x 16 = 80.
Лишь только тогда, когда ученик приобретает опыт в решении таких задач поэтапно, можно показать ему решение подобной задачи обычной пропорцией. 3 маляра за 5 дней выполнят работу,
которую можно измерить как 3 х 5 человеко-дней. Можно пояснить, что человеко-дни – единица, с помощью которой учитывается рабочее время на производстве. И по условию эта работа
выражается в 60-ти окнах. В задаче требуется узнать, чему равна работа, которая измеряется как 4 х 5 человеко-дней.
Значит, можно составить пропорцию:
Однако надо быть внимательным. В некоторых задачах имеет место быть и обратно пропорциональная зависимость. Если, например, количество рабочих увеличивается, то количество
дней, за которые им надо выполнить заданную работу, уменьшается.
|
Задача 7. 3 маляра за 5 дней могут покрасить 60 окон. За сколько дней 5 маляров смогут покрасить 80 окон? |
|---|
Решение. За 1 день один маляр покрасит 4 окна. А 5 маляров за 1 день – 20 окон. А 80 окон 5 маляров смогут покрасить за 4 дня (80 : 20 = 4).
В заключение обзора сложных задач на пропорцию и методов их решения рассмотрим задачу, с четырьмя величинами. Такие задачи сегодня могут встречаться на олимпиадах.
Но было время, когда они входили в курс школьной математики. Например, в учебнике Киселева (который сейчас доступен в Интернете), есть такая задача:
|
Задача 8. (из «Арифметики» А.П. Киселева). На 5 одинаковых керосинок, горевших 24 дня по 6 часов ежедневно, израсходовано 120 л керосина. На сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день? |
|---|
Решение. С тем, чтобы не запутаться в условии, выпишем все данные в виде таблички. Надо отметить, что различного рода таблицы при решении
математических задач, это скорее изобретение советского времени. В учебнике Киселева таблицы отсутствуют, а условие записано двумя строчками. Последуем его примеру:
Далее, если следовать логике решений задач, приведённых на этой странице, а также логике Киселева, решим задачу поэтапно. Сначала решим такую задачу: На сколько дней
хватит 216 л керосина, если те же 5 керосинок будут гореть по 6 часов в день? То есть:
То есть 216 л керосина хватит на 43,2 дня, если будет работать 5 керосинок.
Теперь найдём, на сколько дней хватит 216 л керосина, если керосинок будет не 5, а 9. То есть, если 5 керосинок могут работать 43,2 дня, то 9 керосинок меньше в 1,8 раза
(9 : 5 = 1,8). То есть 9 керосинок, работая по 6 часов в день при запасе в 216 литров, проработают 24 дня.
Осталось найти, на сколько дней хватит 216 л керосина, если 9 таких же керосинок будут гореть по 8 часов в день. То есть:
Таким образом,
Все выполненные действия можно записать одной дробью и сократить ее:
Хочу надеяться, что способы решения нестандартных задач на пропорцию, изложенные в этой статье, помогут пятиклассникам и шестиклассникам, стремящимся изучить материал,
который выходит за рамки программы обычной школы, но который может быть полезен при поступлении в математические лицеи.
© Александр Анатольевич, репетитор по математике в Москве, 8-968-423-9589.

Имею большой опыт работы репетитором. За два десятилетия выработаны собственные методики занятий. Окончил технический ВУЗ – Московский автомобильно-дорожный институт в 1987 г.
Еще в институте оказывал помощь однокурсникам по высшей математике. Репетиторством занимаюсь с 1998 г. За это время мною подготовлено к различным экзаменам более 200 учеников.
Специализируюсь на подготовке в лицеи и математические школы, готовлю к сдаче ОГЭ и ЕГЭ. Занимаюсь также сопровождением школьной программы — подготовкой к контрольным
и самостоятельным работам. Прививаю навыки быстрого устного счета, рассматриваю с учениками логические и нестандартные задачи, направленные на воспитание интереса к предмету,
на развитие логического мышления.